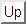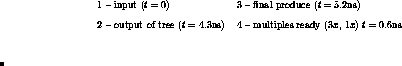
Figure 2: An ECL
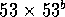 (IEEE standard) multiply in 5.2ns
(latency). The
(IEEE standard) multiply in 5.2ns
(latency). The 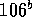 addition at the multiply end takes 850ps.
addition at the multiply end takes 850ps.

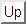

In the area of floating-point multiplication, we have completed two separate studies.
The first concentrated on the use of regular counters, after the work of Santori [3]. This study developed two structures for partial-product reduction for IEEE standard floating point multiplication, leading to structured layouts. Such layouts are desirable because they require shorter wires and therefore support faster operation. The former approach uses a reduction scheme based on a 28/5 counter followed by 55/4 counters. The latter uses a novel family of counters, called 9/2, 6/2, and 4/2 respectively. Both approaches use 3/2 counters as basic building blocks.
We have developed automatic programs for synthesizing the layout of these two structures. The programs are portable across different, but similar, circuit technologies. We have implemented two sample chips, one for each style, in BiCMOS technology. The 28/5 approach had delay of 10ns, while the 9/2 approach had delay of 7ns.
In the second multiplication study, we have developed a scheme based upon a redundant 3-bit Booth encoding of the multiplier. This redundant encoding reduces the number of partial products to be summed by one-third over a full (53 bit) tree partial product summation, but it avoids the requirement of forming plus or minus three multiples of the multiplicand. Coupled to the multiplier encoding, we have developed techniques that allow us to handle irregular counter implementations of the partial product tree. State-of-the-art implementations of partial product trees have focused on 4-2 and similar approaches that provide a regularity in wiring of the partial product tree. We have shown with this work that it is possible to use irregular implementations based upon 3-2 counters with the assistance of CAD tools, which automatically optimize the routing and path length through the partial product tree. Using the combined techniques of the redundant multiplier encoding, and the CAD-assisted layout of the partial product tree, we have implemented a full IEEE floating-point multiplier. This is being implemented now in ECL with the sponsorship of SUN Microsystems. The full multiplier is expected to have an overall delay of five nanoseconds (see Figure 2).
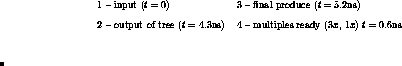
Figure 2: An ECL 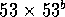 (IEEE standard) multiply in 5.2ns
(latency). The
(IEEE standard) multiply in 5.2ns
(latency). The 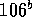 addition at the multiply end takes 850ps.
addition at the multiply end takes 850ps.